转载：

一个集合 XX 的仿射变换为：

f(x)=Ax+b,x∈X

它的几何意义是对一个图形进行：

缩放（Scale）、平移(transform)、旋转(rotate)、反射（reflection, 对图形照镜子）、错切(shear mapping，感觉像是一个图形的倒影)

或者它们的任意组合

维基百科中的一个图很好诠释了各种仿射变换：

仿射变换中集合中的一些性质保持不变：

（1）凸性

（2）共线性：若几个点变换前在一条线上，则仿射变换后仍然在一条线上

（3）平行性：若两条线变换前平行，则变换后仍然平行

（4）共线比例不变性：变换前一条线上两条线段的比例，在变换后比例仍然步

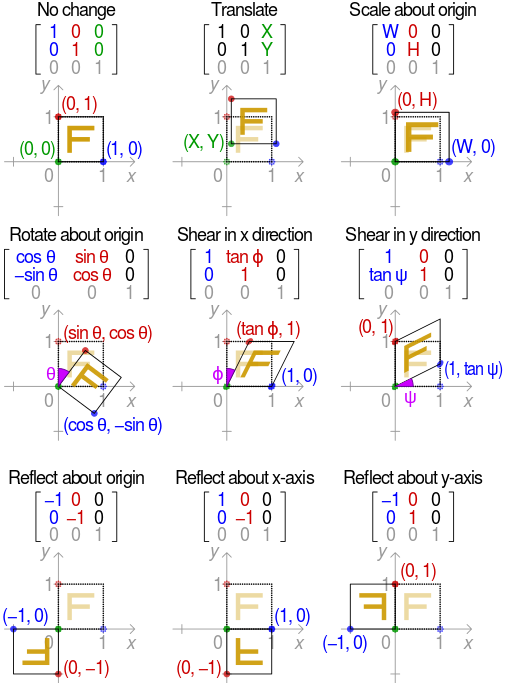
注：所有的三角形都能通过仿射变化为其他三角形，所有平行四边形也能仿射变换为另一个平行四边形。

---------------------

作者：心态与做事习惯决定人生高度

来源：CSDN

原文：https://blog.csdn.net/robert_chen1988/article/details/80498805

版权声明：本文为博主原创文章，转载请附上博文链接！